ডাকবাংলা

অঙ্ক বা বিজ্ঞানশাস্ত্রে যে-সমস্ত নামজাদা ধ্রুবকের কথা আমরা ইশকুল-কলেজে পড়ি, তাদের মধ্যে সবচাইতে প্রাচীন বোধ করি ‘পাই’। মনে আছে, নিশ্চয়ই ছেলেবেলায় এর মান ২২/৭ ধরে বিস্তর অঙ্ক করেছি। আর একটু বড় হয়ে জেনেছি যে আসলে এর মান ৩.১৪১৫৯… এমনি করে চলতেই থাকে— শেষ পাওয়া যায় না। আজ থেকে প্রায় চার হাজার বছর আগে, মানবসভ্যতার সূর্য যখন পুব দিগন্তে সবেমাত্র উঁকি দিয়েছে, ব্যাবিলনের মানুষ এই ধ্রুবকের মান বের করার জন্য প্রথম আঁক কষতে বসে গেছিল। প্রত্নতাত্ত্বিকরা সেইসব অঙ্কের খাতা, মানে, পোড়ামাটির ফলক খুঁজে পেয়েছেন। সেখানে দেখা যাচ্ছে, তীরের মতো আকৃতির কীলক লিপিতে নানারকম আঁকিবুঁকি কেটে ‘পাই’-এর মান নির্ণয়ের চেষ্টা হয়েছে— হ্যাঁ, তার নাম অবিশ্যি তখন ‘পাই’ হয়নি। গ্রিক সভ্যতার তখনও মেলা দেরি। গ্রিক বর্ণ আসবে কোত্থেকে?

এরই কাছাকাছি সময়ে সামান্য দক্ষিণে আর এক প্রাচীন সভ্যতা ছিল মিশর। পিরামিডের দেশও অঙ্কচর্চায় যে পিছিয়ে ছিল না, তার প্রমাণ হিসাবে দাঁড়িয়ে আছে স্বয়ং অতিকায় পিরামিডের দল। অমন বিশালাকৃতির স্থাপত্য যে অমন নির্ভুলতার সাথে নিখুঁতভাবে তৈরি হয়েছে, তা জ্যামিতি আর ত্রিকোণমিতি ছাড়া অসম্ভব। প্রাচীন মিশরের গণিতচর্চার প্রত্যক্ষ প্রমাণ দেখা যাবে ব্রিটিশ মিউজিয়ামে সযত্নে রাখা ‘রাইন্ড প্যাপিরাস’-এ।  আঠারোশো আটান্ন সালে অ্যালেক্সান্ডার হেনরি রাইন্ড নামে এক স্কটিশ প্রত্নসংগ্রাহক মিশরের লাক্সরের থেকে একটা প্রাচীন প্যাপিরাস কেনেন। হায়ারোগ্লিফিক্সে লেখা এই প্যাপিরাস প্রায় সাড়ে তিন হাজার বছরের পুরনো। অনেক পরে, বিংশ শতাব্দীতে যখন এর অর্থ উদ্ধার করা হয়, দেখা যায় যে এর মধ্যে সাতাশিখানা অঙ্ক কষা আছে। তার মধ্যে একটা হল বৃত্তের ক্ষেত্রফল নির্ণয়। আর বৃত্তের ক্ষেত্রফল নির্ণয়ের জন্য দরকার ‘পাই’।

এত অবধি পড়ে আপনার মনে প্রশ্ন জাগতেই পারে যে সেই সভ্যতার আদি লগ্ন থেকে মানুষের মাথায় এমন ‘পাই’-এর বাই চড়েছিল কেন? কী এমন ম্যাজিক লুকিয়ে আছে এর মধ্যে? হকের প্রশ্ন— তাই এর উত্তর খুঁজে নেওয়া যাক বাকি গপ্পের আগে।

আমাদের জগৎসংসারে সমস্ত কিছুই চলে নির্দিষ্ট কিছু নিয়মে। প্রকৃতি ঠাকরুন সবার কান ধরে বলে দিয়েছেন— ‘চলো নিয়মমতে’। আর আমরা, আমাদের জ্ঞাত পরিধির মধ্যে একমাত্র বুদ্ধিমান জীব, সেই সমস্ত নিয়মের ব্যাখ্যা বের করার জন্য তৎপর হয়ে উঠে পড়ে লেগেছি সেই আদি যুগ থেকে। মানবসভ্যতার প্রথমদিকে, যখন মানুষ ঘর বাঁধতে শেখেনি, কাপড় পরতে জানত না, তখনও নিজেদের প্রয়োজনে, সহজাত প্রবৃত্তির ঠেলায় পড়ে অনেক কিছু আবিষ্কার করে ফেলেছে— যেমন শিকার করার জন্য পাথরের অস্ত্র (না কি আত্মরক্ষার জন্য? না কি, নিজের অধিকার বুঝে নেওয়ার জন্য? কে জানে!), শীতের হাত থেকে বাঁচার জন্য আগুন, দ্রুত বেগে এগিয়ে চলার জন্য চাকা, এমন আরও কত কিছু। এই সমস্ত প্রাথমিক চাহিদা পূরণ হওয়ার পর মানুষের বুদ্ধি যখন বিবর্তনের নিয়মে আর একটু বাড়ল, তখন তার ভাবনা হল এই সমস্ত কিছুকে আর একটু ভাল করা যায় কীভাবে? আগুনের জোর কী করে বাড়ানো যায়, চাকাকে আরও কিছুটা মসৃণ করা যায় কি না, আরও ঝকঝকে তীক্ষ্ণ ফলাওয়ালা অস্ত্র বানাতে গেলে কী করতে হবে? আর এই ভাবনা থেকেই জন্ম নিল আদি ইঞ্জিনিয়ারিং— এবং সেই প্রযুক্তিবিদ্যাকে আরও ফলপ্রদ করার জন্য মানুষ ভাবল ‘দেখতে হবে কোত্থেকে আর কী করে, রস জমে এই প্রপঞ্চময় বিশ্বতরুর শিকড়ে’— বাড়ল এই জগৎসংসারকে নিয়ে তার কৌতূহল। সেই থেকে আমরা এখনও অবধি নানারকম ‘সত্য’কে খুঁজেই চলেছি— চারিপাশে যা কিছু ঘটে চলেছে, সমস্ত কিছুর ব্যাখ্যা পাওয়াই একজন বিজ্ঞানমনষ্ক মানুষের একমাত্র অভিপ্রায়।

যাই হোক, তা মানুষ যখন সেই প্রাচীনকালে তার পারিপার্শ্বিক নিয়ে ভাবতে শুরু করল— তখন তার চোখে ধরা পড়ল প্রকৃতিতে ছড়িয়ে থাকা নানাবিধ জ্যামিতিক আকার। প্রযুক্তিগত সুবিধার জন্য জ্যামিতিক আকার সম্পর্কে ধারণা প্রয়োজনীয় হয়ে দাঁড়াল। দৈর্ঘ্য মাপার নানারকম একক তৈরি হল। কিন্তু বাকি সমস্তরকম জ্যামিতিক আকারকে মেপে ফেলা গেলেও গোল বাধল বৃত্তের বেলায়। তার ব্যাস আর পরিধির মধ্যে একটা সমানুপাতিক সম্পর্কে যে আছে, সেটা স্পষ্ট— কিন্তু পরিধি যে ব্যাসের ঠিক কতগুণ আর বৃত্তের ক্ষেত্রফলই বা কত, সেটা মাপা একটু মুশকিল দেখা গেল। অতএব বুদ্ধি খাটানো দরকার।

ব্যাবিলন থেকে পাওয়া যে-মৃৎফলকের কথা শুরুতে বলছিলাম, তার কথা বলি এইবেলা। সেখানে দেখা যাচ্ছে একটা বৃত্ত আঁকা, উপরে লেখা ৩, মাঝে লেখা ৪৫ আর ডানদিকে ৯।

দেখে বেশ একটা গুপ্তধনের সংকেত মনে হতেই পারে। কিন্তু প্রত্নতত্ত্ববিদ এবং বৈজ্ঞানিকদের মতে এ হল ওই বৃত্তের ক্ষেত্রফল নির্ণায়ক একটা অঙ্ক। এবং এই অঙ্ক থেকে বিজ্ঞানীকুলের অনুমান যে, সুমেরীয়দের মতে বৃত্তের পরিধি এবং ব্যাসের যে-অনুপাত, যাকে ‘পাই’ দিয়ে প্রকাশ করা হয়, তার মান ছিল তিন।

আমাদের ভারতবর্ষের প্রাচীন মুনিঋষিরাও যে ‘পাই’-এর মান তিন ধরেই চলতেন, তার প্রমাণ রয়েছে মহাভারতের ভীষ্মপর্বে। সঞ্জয় যখন ধৃতরাষ্ট্রকে কুরুক্ষেত্রর যুদ্ধের লাইভ রিলে করছিলেন, তখন যুদ্ধের কমেন্টারির ফাঁকে-ফাঁকে সমগ্র জম্বুদ্বীপ, আকাশের গ্রহ-নক্ষত্র ইত্যাদি নিয়েও অনেক কিছু বলছিলেন। যেমন ক্রিকেট ধারাভাষ্যের সময়ে দুই ওভারের মাঝের বিরতিতে হর্ষ ভোগলে কিংবা সুনীল গাভাসকার প্রায়ই নানাবিধ অক্রিকেটীয় বাক্যালাপ করে থাকেন আর কি! এক জায়গায় যখন বোধহয় যুদ্ধের ফাঁকে পাণ্ডব-কৌরবরা একটু জিরিয়ে-টিরিয়ে নিচ্ছিল, ধৃতরাষ্ট্র সঞ্জয়কে জিজ্ঞেস করছেন যে, আকাশের রাহু, চাঁদ আর সূর্যর সম্পর্কে কিছু বলো দেখি। উত্তরে সঞ্জয় বলছেন, হে কুরুশ্রেষ্ঠ, রাহুর কথা যখন জিজ্ঞেসই করলেন, বলে রাখি যে রাহু আকৃতিতে গোলাকার, ব্যাস বারো হাজার যোজন এবং এর পরিধি ছত্রিশ হাজার যোজন। চাঁদের সাইজ একটু ছোটো— ব্যাস এগারো হাজার যোজন আর পরিধি তেত্রিশ হাজার। আর সূর্যের আকৃতি আরও ছোট। ব্যাস মোটে দশ হাজার যোজন এবং পরিধি তিরিশ হাজার যোজন। অতএব সঞ্জয়ের হিসাবে ‘পাই’-এর মান যদি হয় তিন তাহলে তাঁর বর্ণিত রাহু, চন্দ্র এবং সূর্যের ব্যাস এবং পরিধির হিসাব মিলে যাচ্ছে।

এই দিক থেকে প্রাচীন মিশরীয়দের গাণিতিক প্রতিভা এগিয়ে ছিল বেশ কয়েক কদম। বৃত্তের ক্ষেত্রফল পরিমাপ করার জন্য একটা কৌশল বের করেছিলো তারা। রাইন্ড প্যাপিরাসের পঞ্চাশ নম্বর প্রশ্নটা এরকম— একটি বৃত্তাকার ক্ষেত্রের ব্যাস ৯ খেত (১ খেত = ৫২.৩ মিটার) হলে, তার ক্ষেত্রফল কত? এর নীচে উত্তর লেখা আছে— ৯ খেতের থেকে এর ১/৯ অংশ, অর্থাৎ ১ খেত বাদ দিলে পড়ে থাকে ৮ খেত। একে ৮ দিয়ে গুণ করলে দাঁড়ায় ৬৪— অর্থাৎ এই বৃত্তের ক্ষেত্রফল ৬৪ সেটজাত (এটাও প্রাচীন মিশরের একটা ক্ষেত্রফল পরিমাপের একক)। এবার আমাদের আধুনিক গণিত অনুযায়ী বৃত্তের ক্ষেত্রফল ব্যাসার্ধের বর্গের সাথে পাইয়ের গুণফলের সমান। অতএব উপরের অঙ্কটার সাথে যদি মেলাই, তাহলে রাইন্ড প্যাপিরাসের রচয়িতার মতে ‘পাই’-এর মান দাঁড়ায় ২৫৬/৮১ অর্থাৎ ৩.১৬ এর মতো। আশ্চর্যের বিষয়, সাড়ে তিন হাজার বছর আগে মিশরীয়দের হিসাব আধুনিক হিসাবে ‘পাই’-এর মানের খুবই কাছাকাছি। কিন্তু অমন আজব ফর্মুলাটা মিশরীয়রা পেল কোথা থেকে?

এর উত্তর আছে ওই প্যাপিরাসেই। দু’পাতা আগে আটচল্লিশ নম্বর অঙ্কে।

সেখানে একটা অষ্টভুজের ক্ষেত্রফল বের করা হয়েছে। একটা বর্গক্ষেত্রের মধ্যে এই অষ্টভুজকে এঁকে মিশরীয় গণিতজ্ঞ দেখিয়েছেন যে বর্গক্ষেত্রের ক্ষেত্রফলের মোটামুটি একের নয় ভাগ বাদ দিলে এই অষ্টভুজটার ক্ষেত্রফল পাওয়া যাবে। আর এই অষ্টভুজের ক্ষেত্রফল তার শীর্ষবিন্দুগুলিকে স্পর্শ করে আঁকা বৃত্তের খুব কাছাকাছি।

অতএব বর্গক্ষেত্রের মধ্যে যদি একটা বৃত্ত আঁকা হয়, যা বর্গক্ষেত্রের বাহুগুলিকে স্পর্শ করে থাকবে, তাহলে সেই বৃত্তের ক্ষেত্রফল হবে বর্গের ক্ষেত্রফলের নয় ভাগের আটভাগ। এবার পাতা উলটে পঞ্চাশ নম্বর অঙ্কে ফেরত যাওয়া যাক। বৃত্তের ব্যাস যদি ৯ হয়, তার অর্থ ওই পরিবেষ্টনকারী বর্গক্ষেত্রের একটা বাহুর দৈর্ঘ্য ৯— বাকিটা জলবৎ তরলং।

বৃত্তের বাইরে এবং ভিতরে বহুভুজ এঁকে তার মাধ্যমে বৃত্তের ক্ষেত্রফল নির্ণয় এবং তার থেকে ‘পাই’-এর মান বের করার এই পদ্ধতি চলেছে প্রায় সপ্তদশ শতাব্দী অবধি। অবশ্যই প্রযুক্তি এবং বিজ্ঞানের উন্নতির সাথে সুবিধা হয়েছে হিসাব করার। অষ্টভুজ বা বর্গক্ষেত্রর জায়গায় আরও অনেক বাহুবিশিষ্ট বহুভুজের ব্যবহারের মাধ্যমে অনেক বেশি সূক্ষ্মতার সাথে ‘পাই’-এর মান নির্দিষ্ট করা গেছে। যেমন বিখ্যাত বৈজ্ঞানিক আর্কিমিডিস খ্রিষ্টের জন্মের আড়াইশো বছর আগে মিশরীয় পদ্ধতির সাথে পিথাগোরাসের তত্ত্ব যোগ করে বের করেছিলেন ‘পাই’-এর মান। অবিশ্যি একটা নির্দিষ্ট মানের বদলে আর্কিমিডিস বলেছিলেন, ‘পাই’-এর মান ২২/৭-এর কম এবং ২২৩/৭১ এর বেশি হবে। আমরা আর্কিমিডিসের কথামতো ইশকুলে ‘পাই’-এর মান ২২/৭ ধরে কত অঙ্ক করেছি।

এই জ্যামিতির সাহায্যে ‘পাই’-এর মান নির্ণয়ের পদ্ধতিতে পরিবর্তন এল ষোড়শ শতাব্দী— সপ্তদশ শতাব্দীর আশেপাশে। ততদিনে হাজার-হাজার বাহুবিশিষ্ট বহুভুজের মাধ্যমে ‘পাই’-এর মান দশমিকের পর প্রায় পঁয়ত্রিশটা সংখ্যা অবধি বের করে ফেলেছেন অনেকে। পঞ্চদশ শতাব্দী নাগাদ আমাদের দেশের কেরালাতে বিখ্যাত গণিতজ্ঞ মাধব ত্রিকোণমিতির সাইন, কোসাইন ইত্যাদির মাননির্ণায়ক অসীম শ্রেণির (infinite series) আবিষ্কার করেন। অবিশ্যি ‘সাইন’ বা ‘কোসাইন’-এর বদলে তাদের তখন ভারতীয় নাম ছিল যথাক্রমে ‘জ্যা’ এবং ‘কোটিজ্যা’। মাধব এই ‘জ্যা’ এবং ‘কোটিজ্যা’-এর অসীম শ্রেণি থেকে বৃত্তের পরিধি এবং ব্যাসের অনুপাত অর্থাৎ ‘পাই’কেও প্রকাশ করেছিলেন আর একটা অসীম শ্রেণি হিসাবে। এর প্রায় তিনশো বছর পর ইউরোপে অনুরূপ পদ্ধতিতে ‘পাই’-এর মান বের করার চেষ্টা করেন বেশ কিছু বৈজ্ঞানিক। তাঁদের মধ্যে সবচেয়ে বিখ্যাত দুইজন— গটফ্রিড উইলহেলম লিবনিজ এবং স্যার আইজ্যাক নিউটন।

লিবনিজ এবং নিউটন— দুজনেই অসীম শ্রেণির সাহায্যে ‘পাই’-এর মান গণনা করলেও দুইজনের পদ্ধতি আলাদা ছিল। নিউটনের ভুরি-ভুরি আবিষ্কারের মধ্যে একটা বিখ্যাত তত্ত্ব ছিল ‘দ্বিপদ উপপাদ্য’ বা ‘বাইনোমিয়াল থিয়োরেম’। ষোলশো ছেষট্টি সালে ইংল্যান্ডে বিউবনিক প্লেগ মহামারীর আকারে ছড়িয়ে পড়েছে, গোটা দেশে ‘লকডাউন’-এর মতোই অবস্থা। নিউটনও গৃহবন্দি। কিন্তু প্রতিভাবান মানুষের মস্তিষ্কে তো আর ‘লকডাউন’ হয় না। বাড়ি বসে খাতার পাতায় আঁক কষে আবিষ্কার করলেন বিখ্যাত ‘দ্বিপদ উপপাদ্য’ আর এই ‘দ্বিপদ উপপাদ্য’র খুব সহজ প্রয়োগে ‘পাই’-এর মান।

অন্যদিকে লিবনিজ গণনা করেন একদম মাধবের পদ্ধতিতে। না জেনেই অবিশ্যি। আর ইউরোপীয় বলে স্বীকৃতিও পেয়ে গেছেন চটজলদি। তাই এই সিরিজের নাম ‘লিবনিজ সিরিজ’ হিসাবেই বিখ্যাত জগৎজুড়ে। এদিকে আরও তিনশো বছর আগে একই জিনিস আবিষ্কার করেও মাধবের নাম বিস্মৃতির আড়ালে— তাঁর লেখা বই তো কবেই হারিয়ে গেছে পৃথিবীর বুক থেকে। ভরসা শুধু তাঁর অনুগামীদের লেখা কিছু বই ও টীকা।

অষ্টাদশ শতাব্দীতে ইউরোপে ‘পাই’-এর মান বের করা ছাড়াও আর কয়েকটা উল্লেখযোগ্য কাজ হয়। কলকাতাতে ‘এশিয়াটিক সোসাইটি’র প্রতিষ্ঠাতা বিখ্যাত স্যার উইলিয়াম জোন্সকে মনে আছে নিশ্চয়ই? মজার ব্যাপার হলো তাঁর বাবার নামও ছিল ‘উইলিয়াম জোন্স’। এ অবিশ্যি সেকালে ইউরোপীয় বিশেষ করে ব্রিটিশদের মধ্যে হামেশাই হত। এই সিনিয়ার উইলিয়াম জোন্স ছিলেন এক বিখ্যাত গণিতজ্ঞ। নিউটন এবং এডমন্ড হ্যালির বন্ধু। সতেরোশো ছয় সালে তিনি Synopsis Palmariorum Matheseos নামে একটা অঙ্কের বই প্রকাশ করেন। সেখানে নানাবিধ তত্ত্বকথার মধ্যে কিছু কথা ছিল ‘পাই’-এর মান নির্ণয় প্রসঙ্গেও। এবং সেখানেই সর্বপ্রথম গ্রিক বর্ণ ‘পাই’ ব্যবহার করেন বৃত্তের পরিধি এবং ব্যাসের অনুপাতকে প্রকাশ করার জন্য। এর কয়েক দশক পরে আর এক বিখ্যাত বৈজ্ঞানিক লিওনার্ড অয়লার এই ‘পাই’ নামটাকে আরও প্রচারিত করে বিখ্যাত করে ফেলেন জ্ঞানসমাজে।

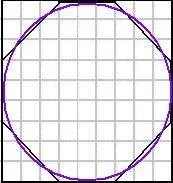
নামকরণের পর অষ্টাদশ শতকের দ্বিতীয় ভাগে ‘পাই’-এর ব্যাপারে আরও একটা উল্লেখযোগ্য আবিষ্কার করেন সুইস বৈজ্ঞানিক জোহান ল্যাম্বার্ট। এতক্ষণে পাঠক নিশ্চয়ই খেয়াল করেছেন যে ‘পাই’-এর মান বের করার খেলা হাজার-হাজার বছর ধরে চলার পরেও তার শেষ পাওয়া যায়নি। একজন দশমিকের পর দশটা সংখ্যা অবধি নির্ণয় করে যান তো তার পরে আর একজন এসে আরও একশোটা সংখ্যা অবধি মান বের করেন। রবি ঠাকুর হয়তো এই কথা ভেবেই লিখেছিলেন, মধুর, তোমার শেষ যে না ‘পাই’। এমন করে মাধব-লিবনিজের অসীম শ্রেণির সাহায্যে অষ্টাদশ শতকে দশমিকের পর একশো ঘর অবধি মান বেরিয়ে গেছে। কিন্তু তার কোনও অন্ত নেই। ল্যাম্বার্ট সতেরোশো একষট্টি সালে প্রমাণ করতে সক্ষম হন যে ‘পাই’ আসলে একটা অমূলদ সংখ্যা (irrational number), অর্থাৎ একে দুটি সংখ্যার ভগ্নাংশ হিসাবে কখনওই প্রকাশ করা যাবে না এবং এটা একটা এমন সংখ্যা যার মান সারাজীবন ধরে হিসাব করে গেলেও শেষ হবার নয়। দশমিকের পর গড়গড়িয়ে চলতেই থাকবে।

এর পর ‘পাই’-এর মান নির্ণয়ের যত চেষ্টা হয়েছে সবই প্রায় এই অসীম শ্রেণির সাহায্যে। এ-ব্যাপারে নবীনতম আবিষ্কারটার কথা বলে এ-লেখায় দাঁড়ি টানব।

এ-বছর জুন মাসে ইন্ডিয়ান ইন্সটিটিউট অফ সায়েন্স, ব্যাঙ্গালোরের দুই বাঙালি পদার্থবিদ— অর্ণব সাহা এবং অনিন্দ্য সিনহা একটা গবেষণাপত্র প্রকাশ করেছেন ‘ফিজিক্যাল রিভিউ লেটারস’-এ। গবেষণার বিষয় ছিল হাই এনার্জি ফিজিক্স, অর্থাৎ কিনা উচ্চশক্তিসম্পন্ন পারমাণবিক কণাদের নিয়ে। ফেইনম্যান ডায়াগ্রাম এবং অয়লার-বিটা ফাংশনের সাহায্যে ওঁরা চেষ্টা করছিলেন পারমাণবিক কণাদের নিজের মধ্যেকার ক্রিয়া-প্রতিক্রিয়া সম্পর্কে নতুন কিছু অনুসন্ধানের। সেই কাজের গাণিতিক হিসাবনিকাশের ফলস্বরূপ এক নতুন অসীম শ্রেণির জন্ম দিয়ে ফেলেছেন তাঁরা, যা কিনা ‘পাই’-এর মান নির্ণয়ে সহায়ক হয়ে দাঁড়িয়েছে। পদার্থবিদ্যায় ব্যবহৃত বিভিন্ন অপেক্ষক বা ফাংশনের মাধ্যমে ‘পাই’-এর মান প্রকাশের এই পদ্ধতি যে বেশ অভিনব তাতে সন্দেহ নেই।

‘পাই’-এর মান নির্ণয়ের এই হাজার-হাজার বছরের খেলায় সেই ব্যাবিলনের পোড়ামাটির ফলক থেকে ‘ফিজিক্যাল রিভিউ লেটারস’-এর পাতা অবধি মানুষের অনুসন্ধিৎসু মন খুঁজে চলেছে এই অদ্ভুত রাশিটার এমন অদ্ভুতুড়ে প্রকৃতির কারণ। একটা বৃত্তের পরিধি আর ব্যাসের অনুপাত যে এমন গোলমেলে একটা জিনিস, তা সাধারণভাবে ভাবলেই ভারি অবাক হতে হয়। আমাদের চারিপাশে ছড়িয়ে থাকা ছোট-ছোট জিনিসের মধ্যে কত যে বিস্ময় লুকিয়ে আছে, তা আমরা হয়তো জানিও না। ভাবলে আরও অবাক হতে হয় যে, যা কিছু দেখি চারদিকে, সমস্ত কিছুর মধ্যেই লুকিয়ে আছে নানারকম গাণিতিক সূত্র, সবই অবিরত নির্দিষ্ট কিছু সূত্র অনুসারে চলেছে। এমনকী আমরা, নিজেরাও তার ব্যতিক্রম নই। প্রকৃতি ঠাকরুনের মতো বড় গণিতবিদ মনে হয় আর হয় না। ‘আওয়ার ম্যাথেম্যাটিকাল ইউনিভার্স’ বইতে এই প্রসঙ্গে ম্যাক্স টেগমার্কের কথা দিয়ে শেষ করি, ‘…our physical world is a mathematical structure. This means that our physical world not only is described by mathematics, but that it is mathematical (a mathematical structure), making us self-aware parts of a giant mathematical object.’

ছবি সৌজন্যে : লেখক